Integration is a core concept of advanced
mathematics, specifically, in the fields of
calculus and
mathematical analysis. Given a
function f(
x) of a real
variable x and an
interval [
a,
b] of the
real line, the
integral 
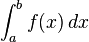
represents the
area of a region in the
xy-plane bounded by the
graph of
f, the
x-axis, and the vertical lines
x=
a and
x=
b.
The term "integral" may also refer to the notion of
antiderivative, a function
F whose derivative is the given function
f. In this case it is called an
indefinite integral, while the integrals discussed in this article are termed
definite integrals. Some authors maintain a distinction between antiderivatives and indefinite integrals.
The principles of integration were formulated by
Isaac Newton and
Gottfried Wilhelm Leibniz in the late seventeenth century. Through the
fundamental theorem of calculus, that they independently developed, integration is connected with
differentiation, and the definite integral of a function can be easily computed once an antiderivative is known. Integrals and derivatives became the basic tools of
calculus, with numerous applications in science and engineering.
A rigorous mathematical definition of the integral was given by
Bernhard Riemann. It is based on a
limiting procedure which approximates the area of a curvilinear region by breaking the region into thin vertical slabs. Beginning in the nineteenth century, more sophisticated notions of integral began to appear, where the type of the function as well as the domain over which the integration is performed has been generalised. A
line integral is defined for functions of two or three variables, and the interval of integration [
a,
b] is replaced by a certain
curve connecting two points on the plane or in the space. In a
surface integral, the curve is replaced by a piece of a
surface in the three-dimensional space. Integrals of
differential forms play a fundamental role in modern
differential geometry. These generalizations of integral first arose from the needs of
physics, and they play an important role in the formulation of many physical laws, notably those of
electrodynamics. Modern concepts of integration are based on the abstract mathematical theory known as
Lebesgue integration, developed by
Henri Lebesgue.
History Integration can be traced as far back as ancient Egypt,
circa 1800 BC, with the
Moscow Mathematical Papyrus demonstrating knowledge of a formula for the volume of a
pyramidal frustum. The first documented systematic technique capable of determining integrals is the
method of exhaustion of
Eudoxus (
circa 370 BC), which sought to find areas and volumes by breaking them up into an infinite number of shapes for which the area or volume was known. This method was further developed and employed by
Archimedes and used to calculate areas for parabolas and an approximation to the area of a circle. Similar methods were independently developed in China around the 3rd Century AD by
Liu Hui, who used it to find the area of the circle. This method was later used by
Zu Chongzhi to find the volume of a sphere.
Significant advances on techniques such as the method of exhaustion did not begin to appear until the 16th Century AD. At this time the work of
Cavalieri with his
method of indivisibles, and work by
Fermat, began to lay the foundations of modern calculus. Further steps were made in the early 17th Century by
Barrow and
Torricelli, who provided the first hints of a connection between integration and
differentiation.
Pre-calculus integration The major advance in integration came in the 17th Century with the independent discovery of the
fundamental theorem of calculus by
Newton and
Leibniz. The theorem demonstrates a connection between integration and differentiation. This connection, combined with the comparative ease of differentiation, can be exploited to calculate integrals. In particular, the fundamental theorem of calculus allows one to solve a much broader class of problems. Equal in importance is the comprehensive mathematical framework that both Newton and Leibniz developed. Given the name infinitesimal calculus, it allowed for precise analysis of functions within continuous domains. This framework eventually became modern
Calculus, whose notation for integrals is drawn directly from the work of Leibniz.
Newton and Leibniz While Newton and Leibniz provided systematic approach to integration, their work lacked a degree of rigour.
Bishop Berkeley memorably attacked
infinitesimals as "the ghosts of departed quantity". Calculus acquired a firmer footing with the development of
limits and was given a suitable foundation by
Cauchy in the first half of the 19th century. Integration was first rigorously formalised, using limits, by
Riemann. Although all piecewise continuous and bounded functions are Riemann integrable on a bounded interval, subsequently more general functions were considered, to which Riemann's definition does not apply, and
Lebesgue formulated a different definition of integral, founded in
measure theory. Other definitions of integral, extending Riemann's and Lebesgue's approaches, were proposed.
Formalising integrals Isaac Newton used a small vertical bar above a variable to indicate integration, or placed the variable inside a box. The vertical bar was easily confused with
or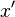
, which Newton used to indicate differentiation, and the box notation was difficult for printers to reproduce, so these notations were not widely adopted.
The modern notation for the indefinite integral was introduced by
Gottfried Leibniz in 1675 (
Burton 1988, p. 359;
Leibniz 1899, p. 154). He derived the integral symbol, "∫", from an
elongated letter S, standing for
summa (Latin for "sum" or "total"). The modern notation for the definite integral, with limits above and below the integral sign, was first used by
Joseph Fourier in
Mémoires of the French Academy around 1819–20, reprinted in his book of 1822 (
Cajori 1929, pp. 249–250;
Fourier 1822, §231). In
Arabic mathematical notation which is written from right to left, an inverted integral symbol
is used
(W3C 2006).
Notation If a function has an integral, it is said to be
integrable. The function for which the integral is calculated is called the
integrand. The region over which a function is being integrated is called the
domain of integration. In general, the integrand may be a function of more than one variable, and the domain of integration may be an area, volume, a higher dimensional region, or even an abstract space that does not have a geometric structure in any usual sense.
The simplest case, the integral of a real-valued function
f of one real variable
x on the interval [
a,
b], is denoted by
The ∫ sign, an elongated "S", represents integration;
a and
b are the
lower limit and
upper limit of integration, defining the domain of integration;
f is the integrand, to be evaluated as
x varies over the interval [
a,
b]; and
dx can have different interpretations depending on the theory being used. For example, it can be seen as merely a notation indicating that
x is the 'dummy variable' of integration, as a reflection of the weights in the Riemann sum, a measure (in Lebesgue integration and its extensions), an infinitesimal (in non-standard analysis) or as an independent mathematical quantity: a
differential form. More complicated cases may vary the notation slightly.
Terminology and notation Integrals appear in many practical situations. Consider a swimming pool. If it is rectangular, then from its length, width, and depth we can easily determine the volume of water it can contain (to fill it), the area of its surface (to cover it), and the length of its edge (to rope it). But if it is oval with a rounded bottom, all of these quantities call for integrals. Practical approximations may suffice at first, but eventually we demand exact and rigorous answers to such problems.
To start off, consider the curve
y =
f(
x) between
x = 0 and
x = 1, with
f(
x) = √
x. We ask:
What is the area under the function
f, in the interval from 0 to 1?
and call this (yet unknown) area the
integral of
f. The notation for this integral will be
.
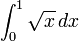As a first approximation, look at the unit square given by the sides
x=0 to
x=1 and
y=
f(0)=0 and
y=
f(1)=1. Its area is exactly 1. As it is, the true value of the integral must be somewhat less. Decreasing the width of the approximation rectangles shall give a better result; so cross the interval in five steps, using the approximation points 0, )/(
q+1).)
Historically, after the failure of early efforts to rigorously define infinitesimals, Riemann formally defined integrals as a
limit of ordinary weighted sums, so that the
dx suggested the limit of a difference (namely, the interval width). Shortcomings of Riemann's dependence on intervals and continuity motivated newer definitions, especially the Lebesgue integral, which is founded on an ability to extend the idea of "measure" in much more flexible ways. Thus the notation
refers to a weighted sum in which the function values are partitioned, with μ measuring the weight to be assigned to each value. (Here
A denotes the region of integration.)
Differential geometry, with its "calculus on
manifolds", gives the familiar notation yet another interpretation. Now
f(
x) and
dx become a
differential form, ω =
f(
x)
dx, a new
differential operator d, known as the
exterior derivative appears, and the fundamental theorem becomes the more general
Stokes' theorem,
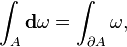
from which
Green's Theorem, the
divergence theorem, and the
fundamental theorem of calculus follow.
More recently, infinitesimals have reappeared with rigor, through modern innovations such as
non-standard analysis. Not only do these methods vindicate the intuitions of the pioneers, they also lead to new mathematics.
Although there are differences between these conceptions of integral, there is considerable overlap. Thus the area of the surface of the oval swimming pool can be handled as a geometric ellipse, as a sum of infinitesimals, as a Riemann integral, as a Lebesgue integral, or as a manifold with a differential form. The calculated result will be the same for all.
Introduction There are many ways of formally defining an integral, not all of which are equivalent. The differences exist mostly to deal with differing special cases which may not be integrable under other definitions, but also occasionally for pedagogical reasons. The most commonly used definitions of integral are Riemann integrals and Lebesgue integrals.
Formal definitions Main article: Riemann integral Riemann integral Main article: Lebesgue integral Lebesgue integral Although the Riemann and Lebesgue integrals are the most important definitions of the integral, a number of others exist, including:
The
Riemann-Stieltjes integral, an extension of the Riemann integral.
The
Lebesgue-Stieltjes integral, further developed by
Johann Radon, which generalizes the
Riemann-Stieltjes and
Lebesgue integrals.
The
Daniell integral, which subsumes the
Lebesgue integral and
Lebesgue-Stieltjes integral without the dependence on
measures.
The
Henstock-Kurzweil integral, variously defined by
Arnaud Denjoy,
Oskar Perron, and (most elegantly, as the gauge integral)
Jaroslav Kurzweil, and developed by
Ralph Henstock.
Other integrals Linearity A number of general inequalities hold for Riemann-integrable
functions defined on a
closed and
bounded interval [
a,
b] and can be generalized to other notions of integral (Lebesgue and Daniell).
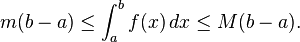
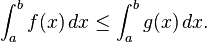
This is a generalization of the above inequalities, as M(b − a) is the integral of the constant function with value M over [a, b].
If f is Riemann-integrable on [a, b] then the same is true for |f|, and
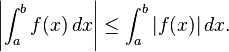
Moreover, if f and g are both Riemann-integrable then f are also Riemann integrable and the following Minkowski inequality holds: 
Inequalities for integrals
In this section f is a real-valued Riemann-integrable function. The integral
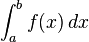
over an interval [a, b] is defined if a < b. This means that the upper and lower sums of the function f are evaluated on a partition a = x0 ≤ x1 ≤ . . . ≤ xn = b whose values xi are increasing. Geometrically, this signifies that integration takes place "left to right", evaluating f within intervals [x i , x i +1] where an interval with a higher index lies to the right of one with a lower index. The values a and b, the end-points of the interval, are called the limits of integration of f. Integrals can also be defined if a > b:
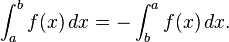
This, with a = b, implies:
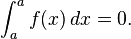
The first convention is necessary in consideration of taking integrals over subintervals of [a, b]; the second says that an integral taken over a degenerate interval, or a point, should be zero. One reason for the first convention is that the integrability of f on an interval [a, b] implies that f is integrable on any subinterval [c, d], but in particular integrals have the property that:
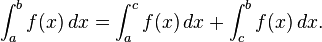
With the first convention the resulting relation
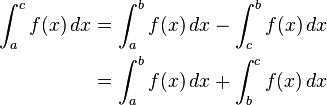
is then well-defined for any cyclic permutation of a, b, and c.
Instead of viewing the above as conventions, one can also adopt the point of view that integration is performed on oriented manifolds only. If M is such an oriented m-dimensional manifold, and M' is the same manifold with opposed orientation and ω is an m-form, then one has (see below for integration of differential forms):
Reversing limits of integration. If a > b then define
Integrals over intervals of length zero. If a is a real number then
Additivity of integration on intervals. If c is any element of [a, b], then Conventions
Main article: Fundamental theorem of calculus Fundamental theorem of calculus
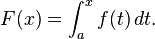
then F is continuous on [a, b]. If f is continuous at x in [a, b], then F is differentiable at x, and F ′(x) = f(x).
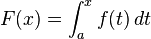
is an anti-derivative of f on [a, b]. Moreover,
Fundamental theorem of calculus. Let f be a real-valued integrable function defined on a closed interval [a, b]. If F is defined for x in [a, b] by
Second fundamental theorem of calculus. Let f be a real-valued integrable function defined on a closed interval [a, b]. If F is a function such that F ′(x) = f(x) for all x in [a, b] (that is, F is an antiderivative of f), then
Corollary. If f is a continuous function on [a, b], then f is integrable on [a, b], and F, defined by Statements of theorems
Extensions
Main article: Improper integral Improper integrals Main article: Multiple integral Multiple integration Main article: Line integral Line integrals Main article: Surface integral Surface integrals Main article: differential form Integrals of differential forms Methods and applications The most basic technique for computing integrals of one real variable is based on the
fundamental theorem of calculus. It proceeds like this:
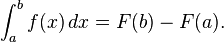
Note that the integral is not actually the antiderivative, but the fundamental theorem allows us to use antiderivatives to evaluate definite integrals.
The difficult step is often finding an antiderivative of
f. It is rarely possible to glance at a function and write down its antiderivative. More often, it is necessary to use one of the many techniques that have been developed to evaluate integrals. Most of these techniques rewrite one integral as a different one which is hopefully more tractable. Techniques include:
Even if these techniques fail, it may still be possible to evaluate a given integral. The next most common technique is
residue calculus, whilst for
nonelementary integrals Taylor series can sometimes be used to find the antiderivative. There are also many less common ways of calculating definite integrals; for instance,
Parseval's identity can be used to transform an integral over a rectangular region into an infinite sum. Occasionally, an integral can be evaluated by a trick; for an example of this, see
Gaussian integral.
Computations of volumes of
solids of revolution can usually be done with
disk integration or
shell integration.
Specific results which have been worked out by various techniques are collected in the
list of integrals.
Choose a function
f(
x) and an interval [
a,
b].
Find an antiderivative of
f, that is, a function
F such that
F' =
f.
By the fundamental theorem of calculus, provided the integrand and integral have no
singularities on the path of integration,
Therefore the value of the integral is
F(
b) −
F(
a).
Integration by substitution Integration by parts Integration by trigonometric substitution Integration by partial fractions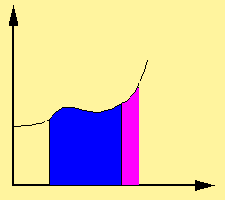 
Computing integrals Main article: Symbolic integration Numerical quadrature Table of integrals - integrals of the most common functions.
Lists of integrals Multiple integral Antiderivative Numerical integration Integral equation Riemann integral Riemann sum Differentiation under the integral sign Product integral
Growth capital is a very flexible type of
financing. The money borrowed under a growth
capital line of
credit can be used for any
corporate purposes. There are no requirements to provide
invoices or other backup material when borrowing under this type of facility, so administration is simplified as well.
Growth capital can be a beneficial way to extend a company's runway between rounds of financing. The extra time can be used to complete additional milestones that will raise the company's valuation, or as insurance to ensure that all intended milestones are successfully accomplished.
The
Court system of Canada is made up of many
courts differing in levels of legal superiority and separated by jurisdiction. Some of the courts are
federal in nature while others are provincial or territorial.
The Canadian constitution gives the federal government the exclusive right to legislate criminal law while the provinces have exclusive control over civil law. The provinces have jurisdiction over the administration of justice in their territory. Almost all cases, whether criminal or civil, start in provincial courts and may be eventually appealed to higher level courts. The quite small system of federal courts only hear cases concerned with matters which are under exclusive federal control, such as immigration. The federal government appoints and pays for both the judges of the federal courts and the judges of the superior-level court of each province. The provincial governments are responsible for appointing judges of the lower provincial ("inferior-level") courts.
This intricate interweaving of federal and provincial powers is typical of the Canadian constitution.
Outline of the Court system Although created by an Act of the
Parliament of Canada in 1875, its decisions could be reviewed by the
Judicial Committee of the Privy Council until 1949 when the
Supreme Court of Canada truly became the final and highest court in the country. The court currently consists of nine justices, which include the
Chief Justice of Canada, and its duties include hearing appeals of decisions from the
appellate courts (to be discussed next) and, on occasion, delivering
references (i.e., the court's opinion) on constitutional questions raised by the federal government. By law, three of the nine justices are appointed from Quebec; because of Quebec's use of
civil law.
Supreme Court of Canada These courts of appeal (as listed below by province and territory in alphabetical order) exist at the provincial and territorial levels and were separately constituted in the early decades of the 20th century, replacing the former Full Courts of the old Supreme Courts of the provinces, many of which were then re-named Courts of Queens Bench. Their function is to review decisions rendered by the superior-level courts and to do references (i.e., deliver a judicial opinion) when requested by a provincial or territorial government. These appellate courts do not normally conduct trials and hear witnesses.
These courts are Canada's equivalent of the Court of Appeal in
England and the various
State Supreme Courts and
US Courts of Appeals in the
United States. Each of the above-listed appellate courts is the highest court from its respective province or territory. A province's chief justice (i.e., highest ranking judge) sits in the appellate court of that province.
Alberta Court of Appeal British Columbia Court of Appeal Manitoba Court of Appeal New Brunswick Court of Appeal Supreme Court of Newfoundland (Court of Appeal) Court of Appeal for the Northwest Territories Nova Scotia Court of Appeal Nunavut Court of Appeal Ontario Court of Appeal Supreme Court of Prince Edward Island - Appeal Division Quebec Court of Appeal Saskatchewan Court of Appeal Court of Appeal of the Yukon Territory Appellate courts of the provinces and territories These courts (as listed below by province and territory in alphabetical order) exist at the provincial and territorial levels. The superior courts are the
courts of first instance for divorce petitions, civil lawsuits involving claims greater than small claims, and criminal prosecutions for "
indictable offences" (i.e., "
felonies" in American legal terminology). They also perform a reviewing function for judgements from the local "inferior" courts and administrative decisions by provincial or territorial government entities such as labour boards, human rights tribunals and licensing authorities.
Furthermore, some of these superior courts (like the one in Ontario) have specialized branches that deal only with certain matters such as family law or small claims. To complicate things further, the Ontario Superior Court of Justice has a branch called the Divisional Court that hears only appeals and judicial reviews of administrative tribunals and whose decisions have greater binding authority than those from the "regular" branch of the Ontario Superior Court of Justice. Although a court, like the Supreme Court of British Columbia, may have the word "supreme" in its name, it is not necessarily the highest court from its respective province or territory.
Court of Queen's Bench of Alberta Supreme Court of British Columbia Court of Queen's Bench of Manitoba Court of Queen's Bench of New Brunswick Supreme Court of Newfoundland and Labrador (Trial Division)
Supreme Court of the Northwest Territories Supreme Court of Nova Scotia Nunavut Court of Justice Ontario Superior Court of Justice Supreme Court of Prince Edward Island - Trial Division
Quebec Superior Court Court of Queen's Bench for Saskatchewan Supreme Court of the Yukon Territory Superior-level courts of the provinces and territories Main article: Provincial Court Provincial and territorial ("inferior") courts The Federal Court and the more specialized Tax Court of Canada exists primarily to review administrative decisions by federal government bodies such as the
immigration board and hear lawsuits under the federal government's jurisdiction such as
intellectual property and
maritime law.
The Federal Court of Appeal hears appeals from decisions rendered by the Federal Court, the Tax Court of Canada and a certain group of federal administrative tribunals like the National Energy Board and the federal labour board. All judges of the Federal Court are
ex officio judges of the Federal Court of Appeal, and vice versa, although it is rare that a judge of one court will sit as a member of the other.
Before 2003, the Federal Court was known as the Federal Court of Canada - Trial Division while the Federal Court of Appeal was known as the Federal Court of Canada - Appeal Division. In turn, the Federal Court of Canada is descended from the old Exchequer Court of Canada created back in 1875.
Although the federal type courts can be said to have the same prestige as the superior courts from the provinces and territories, the federal ones lack the "inherent jurisdiction" (to be explained later) possessed by superior courts such as the Ontario Superior Court of Justice.
Federal Court
Tax Court of Canada
Federal Court of Appeal
Courts of the federal level The "courts martial" are conducted and presided over by military personnel and exist for the prosecution of military personnel, as well as civilian personnel who accompany military personnel, accused of violating the
Code of Service Discipline, which is found in the
National Defence Act (R.S.C. 1985, Chapter N-5) and constitutes a complete code of military law applicable to persons under military jurisdiction.
The decisions of the courts martial can be appealed to the Court Martial Appeal Court of Canada which, in contrast, exists outside the military and is made up of civilian judges. This appellate court is the successor of the Court Martial Appeal Board which was created in 1950, presided over by civilian judges and lawyers, and was the first ever civilian-based adjudicating body with authority to review decisions by a military court. The Court Martial Appeal Court is made up of civilian judges from the Federal Court, Federal Court of Appeal, and the superiour courts of the provinces. The current Chief Justice of the Court Martial Appeal Court (as of September 17, 2004) is Edmond P. Blanchard.
Court Martial Appeal Court of Canada
various military courts called "courts martial"
- General Court Martial
Disciplinary Court Martial
Standing Court Martial
Special General Court Martial 
Courts of military law
Known in Canada as simply "tribunals", these are non-judicial adjudicative bodies, which means that they adjudicate (hear evidence and render decisions) like the courts do BUT are not presided over by judges. Instead, the adjudicators may be experts of the very specific legal field handled by the tribunal (e.g., labour law, human rights law, immigration law, energy law, liquor licensing law, etc.) who hear arguments and evidence provided by lawyers before making a written decision on record. Its decisions can be reviewed by a court through an appeal or a process called "judicial review". The reviewing court may be required to show some deference to the tribunal if the tribunal possesses some highly specialized expertise or knowledge that the court does not have. The degree of deference will also depend on such factors as the specific wording of the legislation creating the tribunal.
Tribunals may take into consideration the Canadian Charter of Rights and Freedoms, which is part of Canada's constitution. The extent to which tribunals may use the Charter in their decisions is a source of ongoing legal debate.
Appearing before some administrative tribunals may feel like appearing in a court, but the tribunal's procedure is relatively less formal than that of the court, and more importantly, the rules of evidence are not as strictly observed. In other words, some evidence that would be inadmissible in a court hearing could be allowed in a tribunal hearing. The presiding adjudicator is normally called "Mister/Madam Chair", and lawyers routinely appear in tribunals advocating a matter for their clients. A person does not require a lawyer to appear before an administrative tribunal. Indeed, many of these tribunals are specifically designed to be less formal than courts. Furthermore, some of these tribunals are part of a comprehensive dispute-resolution system, which may emphasize mediation rather than litigation. For example, provincial human rights commissions routinely use mediation to resolve many human rights complaints without the need for a hearing.
What tribunals all have in common is that they are created by statute, their adjudicators are appointed by government, and they focus on very particular and specialized areas of law. Because some subject matters (e.g., immigration) fall within federal jurisdiction while others (e.g., liquor licensing) in provincial jurisdiction, some tribunals are created by federal law while others are created by provincial law. Yet, there are both federal and provincial tribunals for some subject matters such as unionized labour and "human rights" (in American legal parlance, the "civil rights" of marginalized or/and disadvantaged social groups such as women, racial minorities, the disabled, homosexuals, certain religious groups, etc.).
Most importantly, from a lawyer's perspective, is the fact that the principle of stare decisis does not apply to tribunals. In other words, a tribunal adjudicative could legally make a decision that differs from a past decision, on the same subject and issues, delivered by the highest court in the land. Because a tribunal is not bound by legal precedent, established by itself or by a reviewing court, A tribunal is not court even though it performs an important adjudicative function and contributes to the development of law like a court would do. Although stare decisis does not apply to tribunals, their adjudicators will nonetheless find a prior court decision on a similar subject to be highly persuasive and will likely follow the courts in order to ensure consistency in the law and to prevent the embarrassment of having their decisions overturned by the courts.
Among the federal tribunals, there is a small group of tribunals whose decisions must be appealed directly to the Federal Court of Appeal rather than to the Federal Court Trial Division. These so-called "super tribunals" are listed in Subsection 28(1) of the Federal Court Act (R.S.C. 1985, Chapter F-7) and some examples include the National Energy Board, Canadian International Trade Tribunal, the Competition Tribunal, the Canada Industrial Relations Board (i.e. federal labour board), the Copyright Board, and the Canadian Radio-television and Telecommunications Commission ("CRTC").
Federal and provincial administrative tribunals
These are the superior courts from the provinces and territories as discussed above. The words "inherent jurisdiction" refers to the fact that the jurisdiction of the superior courts is more than just what is conferred by statute. Following the principles of English common law, because the superior courts derive their authority from the Constitution, they can hear any matter unless there is a federal or provincial statute that says otherwise or that gives exclusive jurisdiction to some other court or tribunal. The doctrine of "inherent jurisdiction" gives superior courts greater freedom than statutory courts (to be explained next) to be flexible and creative in the delivering of legal remedies and relief.
Courts of inherent jurisdiction
These courts include the Supreme Court of Canada, the different types of federal courts, the various appellate courts from the provinces and territories, and the numerous low level "provincial" courts. Their decision-making power is granted by either the federal parliament or a provincial legislature.
The word "statutory" refers to the fact that these courts' powers are derived from a type of legislation called a statute and is defined and limited by a statute. A statutory court cannot try cases in areas of law that are not mentioned or suggested in the statute. In this sense, statutory courts are similar to non-judicial adjudicative bodies such as administrative tribunals, boards, commissions, etc. which are created and given limited power by legislation. The practical implication of this is that a statutory court cannot provide a type of legal remedy or relief that is not expressly or implicitly referred to in its enabling or empowering statute.
Statutory courts
Main article: Judicial appointments in Canada
Purity is the state of being
pure; the opposite of purity is
impurity.
Purity may refer to:
Morality, the concept of human ethics
Black Oil virus, codenamed
Purity in
The X-files Purity Supermarkets, a brand formerly used for a supermarket chain by
Woolworths Limited in Tasmania, Australia
Purity Distilling Company, the company responsible for the Boston molasses disaster
"Purity", a song by the band Slipknot on their self-titled album
Slipknot
In
Hinduism,
Durga (
Sanskrit:
"the inaccessible"
Durga is depicted as a warrior woman riding a lion or a tiger with multiple hands carrying weapons and assuming mudras, or symbolic hand gestures. This form of the Goddess is the embodiment of feminine and creative energy (Shakti).
Durga in the Hindu tradition
The 4 day Durga Puja is the biggest annual festival in Bengal and other parts of Eastern India, but it is celebrated in various forms throughout the Hindu universe.
The day of Durga's victory is celebrated as Vijaya Dashami (East and South India), Dashain (Nepal) or Dussehra (North India) - these words literally mean "the tenth" (day), vijaya means "of-victory". In Kashmir she is worshipped as shaarika (the main temple is in Hari Parbat in Srinagar).
The actual period of the worship however may be on the preceding nine days followed by the last day called Vijayadashami in North India or five days in Bengal, (from the sixth to tenth day of the waxing-moon fortnight). Nine aspects of Durga known as Navadurga are meditated upon, one by one during the nine-day festival by devout shakti worshippers.
In North India, this tenth day, signifying Rama's victory in his battle against the demon Ravana, is celebrated as Dussehra - gigantic straw effigies of Ravana are burnt in designated open spaces (e.g. Delhi's Ram Lila grounds), watched by thousands of families and little children.
In Gujarat it is celebrated as the last day of Navaratri, during which the Garba dance is performed to celebrate the vigorous victory of Mahishasura-mardini Durga.
The Goddess Durga worshipped in her peaceful form as Shree Shantadurga also known as santeri , is the patron Goddess of Goa. She is worshipped by all Goan Hindus irrespective of caste and even by some Christians in Goa.
Goddess Durga is worshipped in many temples of Dakshina Kannada district of Karnataka.
See also
