Tuesday, December 4, 2007


Integration is a core concept of advanced mathematics, specifically, in the fields of calculus and mathematical analysis. Given a function f(x) of a real variable x and an interval [a,b] of the real line, the integral
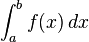
int_a^b f(x),dx
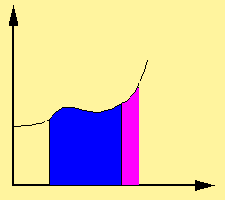
represents the area of a region in the xy-plane bounded by the graph of f, the x-axis, and the vertical lines x=a and x=b.
The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function f. In this case it is called an indefinite integral, while the integrals discussed in this article are termed definite integrals. Some authors maintain a distinction between antiderivatives and indefinite integrals.
The principles of integration were formulated by Isaac Newton and Gottfried Wilhelm Leibniz in the late seventeenth century. Through the fundamental theorem of calculus, that they independently developed, integration is connected with differentiation, and the definite integral of a function can be easily computed once an antiderivative is known. Integrals and derivatives became the basic tools of calculus, with numerous applications in science and engineering.
A rigorous mathematical definition of the integral was given by Bernhard Riemann. It is based on a limiting procedure which approximates the area of a curvilinear region by breaking the region into thin vertical slabs. Beginning in the nineteenth century, more sophisticated notions of integral began to appear, where the type of the function as well as the domain over which the integration is performed has been generalised. A line integral is defined for functions of two or three variables, and the interval of integration [a,b] is replaced by a certain curve connecting two points on the plane or in the space. In a surface integral, the curve is replaced by a piece of a surface in the three-dimensional space. Integrals of differential forms play a fundamental role in modern differential geometry. These generalizations of integral first arose from the needs of physics, and they play an important role in the formulation of many physical laws, notably those of electrodynamics. Modern concepts of integration are based on the abstract mathematical theory known as Lebesgue integration, developed by Henri Lebesgue.

History
Integration can be traced as far back as ancient Egypt, circa 1800 BC, with the Moscow Mathematical Papyrus demonstrating knowledge of a formula for the volume of a pyramidal frustum. The first documented systematic technique capable of determining integrals is the method of exhaustion of Eudoxus (circa 370 BC), which sought to find areas and volumes by breaking them up into an infinite number of shapes for which the area or volume was known. This method was further developed and employed by Archimedes and used to calculate areas for parabolas and an approximation to the area of a circle. Similar methods were independently developed in China around the 3rd Century AD by Liu Hui, who used it to find the area of the circle. This method was later used by Zu Chongzhi to find the volume of a sphere.
Significant advances on techniques such as the method of exhaustion did not begin to appear until the 16th Century AD. At this time the work of Cavalieri with his method of indivisibles, and work by Fermat, began to lay the foundations of modern calculus. Further steps were made in the early 17th Century by Barrow and Torricelli, who provided the first hints of a connection between integration and differentiation.

Pre-calculus integration
The major advance in integration came in the 17th Century with the independent discovery of the fundamental theorem of calculus by Newton and Leibniz. The theorem demonstrates a connection between integration and differentiation. This connection, combined with the comparative ease of differentiation, can be exploited to calculate integrals. In particular, the fundamental theorem of calculus allows one to solve a much broader class of problems. Equal in importance is the comprehensive mathematical framework that both Newton and Leibniz developed. Given the name infinitesimal calculus, it allowed for precise analysis of functions within continuous domains. This framework eventually became modern Calculus, whose notation for integrals is drawn directly from the work of Leibniz.

Newton and Leibniz
While Newton and Leibniz provided systematic approach to integration, their work lacked a degree of rigour. Bishop Berkeley memorably attacked infinitesimals as "the ghosts of departed quantity". Calculus acquired a firmer footing with the development of limits and was given a suitable foundation by Cauchy in the first half of the 19th century. Integration was first rigorously formalised, using limits, by Riemann. Although all piecewise continuous and bounded functions are Riemann integrable on a bounded interval, subsequently more general functions were considered, to which Riemann's definition does not apply, and Lebesgue formulated a different definition of integral, founded in measure theory. Other definitions of integral, extending Riemann's and Lebesgue's approaches, were proposed.

Formalising integrals
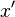Isaac Newton used a small vertical bar above a variable to indicate integration, or placed the variable inside a box. The vertical bar was easily confused with dot{x} or x',!, which Newton used to indicate differentiation, and the box notation was difficult for printers to reproduce, so these notations were not widely adopted.
The modern notation for the indefinite integral was introduced by Gottfried Leibniz in 1675 (Burton 1988, p. 359; Leibniz 1899, p. 154). He derived the integral symbol, "∫", from an elongated letter S, standing for summa (Latin for "sum" or "total"). The modern notation for the definite integral, with limits above and below the integral sign, was first used by Joseph Fourier in Mémoires of the French Academy around 1819–20, reprinted in his book of 1822 (Cajori 1929, pp. 249–250; Fourier 1822, §231). In Arabic mathematical notation which is written from right to left, an inverted integral symbol is used (W3C 2006).

Notation
If a function has an integral, it is said to be integrable. The function for which the integral is calculated is called the integrand. The region over which a function is being integrated is called the domain of integration. In general, the integrand may be a function of more than one variable, and the domain of integration may be an area, volume, a higher dimensional region, or even an abstract space that does not have a geometric structure in any usual sense.
The simplest case, the integral of a real-valued function f of one real variable x on the interval [a, b], is denoted by
int_a^b f(x),dx .
The ∫ sign, an elongated "S", represents integration; a and b are the lower limit and upper limit of integration, defining the domain of integration; f is the integrand, to be evaluated as x varies over the interval [a,b]; and dx can have different interpretations depending on the theory being used. For example, it can be seen as merely a notation indicating that x is the 'dummy variable' of integration, as a reflection of the weights in the Riemann sum, a measure (in Lebesgue integration and its extensions), an infinitesimal (in non-standard analysis) or as an independent mathematical quantity: a differential form. More complicated cases may vary the notation slightly.

Terminology and notation
Integrals appear in many practical situations. Consider a swimming pool. If it is rectangular, then from its length, width, and depth we can easily determine the volume of water it can contain (to fill it), the area of its surface (to cover it), and the length of its edge (to rope it). But if it is oval with a rounded bottom, all of these quantities call for integrals. Practical approximations may suffice at first, but eventually we demand exact and rigorous answers to such problems.
To start off, consider the curve y = f(x) between x = 0 and x = 1, with f(x) = √x. We ask:
What is the area under the function f, in the interval from 0 to 1?
and call this (yet unknown) area the integral of f. The notation for this integral will be
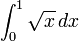int_0^1 sqrt x , dx ,!.
As a first approximation, look at the unit square given by the sides x=0 to x=1 and y=f(0)=0 and y=f(1)=1. Its area is exactly 1. As it is, the true value of the integral must be somewhat less. Decreasing the width of the approximation rectangles shall give a better result; so cross the interval in five steps, using the approximation points 0, )/(q+1).)
Historically, after the failure of early efforts to rigorously define infinitesimals, Riemann formally defined integrals as a limit of ordinary weighted sums, so that the dx suggested the limit of a difference (namely, the interval width). Shortcomings of Riemann's dependence on intervals and continuity motivated newer definitions, especially the Lebesgue integral, which is founded on an ability to extend the idea of "measure" in much more flexible ways. Thus the notation
int_A f(x) , dmu ,!
refers to a weighted sum in which the function values are partitioned, with μ measuring the weight to be assigned to each value. (Here A denotes the region of integration.) Differential geometry, with its "calculus on manifolds", gives the familiar notation yet another interpretation. Now f(x) and dx become a differential form, ω = f(x)dx, a new differential operator d, known as the exterior derivative appears, and the fundamental theorem becomes the more general Stokes' theorem,
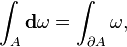
int_{A} bold{d} omega = int_{part A} omega , ,!
from which Green's Theorem, the divergence theorem, and the fundamental theorem of calculus follow.
More recently, infinitesimals have reappeared with rigor, through modern innovations such as non-standard analysis. Not only do these methods vindicate the intuitions of the pioneers, they also lead to new mathematics.
Although there are differences between these conceptions of integral, there is considerable overlap. Thus the area of the surface of the oval swimming pool can be handled as a geometric ellipse, as a sum of infinitesimals, as a Riemann integral, as a Lebesgue integral, or as a manifold with a differential form. The calculated result will be the same for all.

Introduction
There are many ways of formally defining an integral, not all of which are equivalent. The differences exist mostly to deal with differing special cases which may not be integrable under other definitions, but also occasionally for pedagogical reasons. The most commonly used definitions of integral are Riemann integrals and Lebesgue integrals.

Formal definitions

Main article: Riemann integral Riemann integral

Main article: Lebesgue integral Lebesgue integral
Although the Riemann and Lebesgue integrals are the most important definitions of the integral, a number of others exist, including:

The Riemann-Stieltjes integral, an extension of the Riemann integral.
The Lebesgue-Stieltjes integral, further developed by Johann Radon, which generalizes the Riemann-Stieltjes and Lebesgue integrals.
The Daniell integral, which subsumes the Lebesgue integral and Lebesgue-Stieltjes integral without the dependence on measures.
The Henstock-Kurzweil integral, variously defined by Arnaud Denjoy, Oskar Perron, and (most elegantly, as the gauge integral) Jaroslav Kurzweil, and developed by Ralph Henstock. Other integrals

Linearity
A number of general inequalities hold for Riemann-integrable functions defined on a closed and bounded interval [a, b] and can be generalized to other notions of integral (Lebesgue and Daniell).


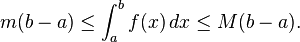
m(b - a) leq int_a^b f(x) , dx leq M(b - a).


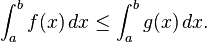
int_a^b f(x) , dx leq int_a^b g(x) , dx.
This is a generalization of the above inequalities, as M(b − a) is the integral of the constant function with value M over [a, b].


int_c^d f(x) , dx leq int_a^b f(x) , dx.


<br /> (fg)(x)= f(x) g(x), ; f^2 (x) = (f(x))^2, ; |f| (x) = |f(x)|.,
If f is Riemann-integrable on [a, b] then the same is true for |f|, and

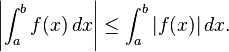
left| int_a^b f(x) , dx right| leq int_a^b | f(x) | , dx.
Moreover, if f and g are both Riemann-integrable then f are also Riemann integrable and the following Minkowski inequality holds: Integral calculus Inequalities for integrals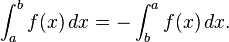
In this section f is a real-valued Riemann-integrable function. The integral
int_a^b f(x) , dx
over an interval [a, b] is defined if a < b. This means that the upper and lower sums of the function f are evaluated on a partition a = x0 ≤ x1 ≤ . . . ≤ xn = b whose values xi are increasing. Geometrically, this signifies that integration takes place "left to right", evaluating f within intervals [x i , x i +1] where an interval with a higher index lies to the right of one with a lower index. The values a and b, the end-points of the interval, are called the limits of integration of f. Integrals can also be defined if a > b:


int_a^b f(x) , dx = - int_b^a f(x) , dx.
This, with a = b, implies:


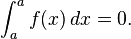
int_a^a f(x) , dx = 0.
The first convention is necessary in consideration of taking integrals over subintervals of [a, b]; the second says that an integral taken over a degenerate interval, or a point, should be zero. One reason for the first convention is that the integrability of f on an interval [a, b] implies that f is integrable on any subinterval [c, d], but in particular integrals have the property that:


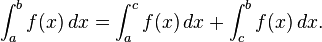
int_a^b f(x) , dx = int_a^c f(x) , dx + int_c^b f(x) , dx.
With the first convention the resulting relation
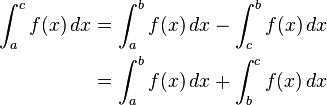
begin{align}<br /> int_a^c f(x) , dx &{}= int_a^b f(x) , dx - int_c^b f(x) , dx <br /> &{} = int_a^b f(x) , dx + int_b^c f(x) , dx<br /> end{align}
is then well-defined for any cyclic permutation of a, b, and c.
Instead of viewing the above as conventions, one can also adopt the point of view that integration is performed on oriented manifolds only. If M is such an oriented m-dimensional manifold, and M' is the same manifold with opposed orientation and ω is an m-form, then one has (see below for integration of differential forms):
int_M omega = - int_{M'} omega ,.

Reversing limits of integration. If a > b then define
Integrals over intervals of length zero. If a is a real number then
Additivity of integration on intervals. If c is any element of [a, b], then Conventions

Main article: Fundamental theorem of calculus Fundamental theorem of calculus


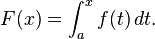
F(x) = int_a^x f(t), dt.
then F is continuous on [a, b]. If f is continuous at x in [a, b], then F is differentiable at x, and F ′(x) = f(x).


int_a^b f(t), dt = F(b) - F(a).


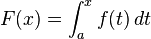
F(x) = int_a^x f(t) , dt
is an anti-derivative of f on [a, b]. Moreover,

int_a^b f(t) , dt = F(b) - F(a).

Fundamental theorem of calculus. Let f be a real-valued integrable function defined on a closed interval [a, b]. If F is defined for x in [a, b] by
Second fundamental theorem of calculus. Let f be a real-valued integrable function defined on a closed interval [a, b]. If F is a function such that F ′(x) = f(x) for all x in [a, b] (that is, F is an antiderivative of f), then
Corollary. If f is a continuous function on [a, b], then f is integrable on [a, b], and F, defined by Statements of theorems

Extensions

Main article: Improper integral Improper integrals

Main article: Multiple integral Multiple integration

Main article: Line integral Line integrals

Main article: Surface integral Surface integrals

Main article: differential form Integrals of differential forms

Methods and applications
The most basic technique for computing integrals of one real variable is based on the fundamental theorem of calculus. It proceeds like this:
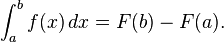
int_a^b f(x),dx = F(b)-F(a).
Note that the integral is not actually the antiderivative, but the fundamental theorem allows us to use antiderivatives to evaluate definite integrals.
The difficult step is often finding an antiderivative of f. It is rarely possible to glance at a function and write down its antiderivative. More often, it is necessary to use one of the many techniques that have been developed to evaluate integrals. Most of these techniques rewrite one integral as a different one which is hopefully more tractable. Techniques include:
Even if these techniques fail, it may still be possible to evaluate a given integral. The next most common technique is residue calculus, whilst for nonelementary integrals Taylor series can sometimes be used to find the antiderivative. There are also many less common ways of calculating definite integrals; for instance, Parseval's identity can be used to transform an integral over a rectangular region into an infinite sum. Occasionally, an integral can be evaluated by a trick; for an example of this, see Gaussian integral.
Computations of volumes of solids of revolution can usually be done with disk integration or shell integration.
Specific results which have been worked out by various techniques are collected in the list of integrals.

Choose a function f(x) and an interval [a, b].
Find an antiderivative of f, that is, a function F such that F' = f.
By the fundamental theorem of calculus, provided the integrand and integral have no singularities on the path of integration,

int_a^b f(x),dx = F(b)-F(a).



Therefore the value of the integral is F(b) − F(a).
Integration by substitution
Integration by parts
Integration by trigonometric substitution
Integration by partial fractions Integral calculus Computing integrals

Main article: Symbolic integration Numerical quadrature

Table of integrals - integrals of the most common functions.
Lists of integrals
Multiple integral
Antiderivative
Numerical integration
Integral equation
Riemann integral
Riemann sum
Differentiation under the integral sign
Product integral
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)